Olá, caros
estudantes! Espero que você e seus familiares continue bem! Nessa quinzena, iniciamos
os estudos de mais um trimestre, UHUUUULLL! Portanto, veremos sobre dilatação térmica
e uma introdução ao estudo dos gases.
Em caso de
qualquer dúvida, entre em contato via whatsapp, ligação ou SMS!
Vamos juntos
nesse ano da aprendizagem!
“O conhecimento é algo que ninguém pode nos tirar. É um
investimento que levamos
para a vida toda. Se dedique e foque em alcançar seus objetivos.”
-
Marianna Moreno.
Dilatação
térmica em nosso cotidiano
Você já deve ter
observado no seu dia a dia algumas situações que envolvem a dilatação térmica.
Por exemplo, se
uma porção de chá muito quente é colocada no interior de um copo de vidro comum,
ele pode trincar. Isso ocorre porque a parte interna do copo é aquecida e se
dilata. Como o vidro é péssimo condutor de calor, a face externa do copo demora
para ser aquecida. É essa diferença de dilatação entre as partes interna e
externa que provoca o trincado do vidro.
Nas calçadas de
cimento, um pedreiro sempre deve dividir o espaço usando ripas de madeira,
pois, se a superfície for grande, com o tempo irá apresentar rachaduras, devido
à dilatação do concreto.
Nas quadras
esportivas com piso de cimento também há juntas de dilatação. É comum lajes de concreto
apresentarem infiltrações. Isso ocorre porque a laje sofre dilatação quando a
temperatura aumenta e contração quando a temperatura
diminui. Podem surgir fissuras na laje, por onde a água entra quando chove. Nas pontes e nos viadutos, devem
ser previstas fendas de dilatação para que a estrutura possa dilatar-se quando
a temperatura aumenta.
Nem todas as pessoas sabem que líquidos muito gelados e comida muito quente podem provocar sérios danos aos dentes. Como os materiais usados nas obturações e os dentes possuem coeficientes de dilatação diferentes, nas variações de temperatura a dilatação ocorre de forma diversa. Se o material da obturação dilatar mais, poderá ocorrer quebra do dente; se dilatar menos, irá se afastar do dente, provocando infiltrações e, consequentemente, cáries.
Imagem de obturações metálicas.
Portanto, a dilatação térmica é o aumento das dimensões do corpo com o aumento da temperatura. Ocorre com quase todos os materiais, no estado sólido, líquido ou gasoso.
Dilatação térmica dos sólidos
Um aumento de temperatura faz com que aumente a vibração e o distanciamento entre os átomos que constituem um corpo sólido. Em consequência disso, ocorre um aumento nas suas dimensões.
Dependendo da dilatação mais significativa em uma determinada dimensão (comprimento, largura e profundidade), a dilatação dos sólidos é classificada em: linear, superficial e volumétrica.
Dilatação Linear
A dilatação linear leva em consideração a dilatação sofrida por um corpo apenas em uma das suas dimensões. É o que acontece, por exemplo, com um fio, em que o seu comprimento é mais relevante do que a sua espessura. Para calcular a dilatação linear utilizamos a seguinte fórmula:
𝜟𝑳 = 𝑳𝒐. 𝜶. 𝜟𝒕
Onde,
ΔL: Variação do comprimento (m ou cm);
L0: Comprimento inicial (m ou cm);
α: Coeficiente de dilatação linear (ºC-1);
Δt: Variação de temperatura (ºC).
Para obter o valor e a unidade do coeficiente de dilatação linear, basta isolar o valor de α na
expressão acima:
Conhecendo a variação de comprimento ΔL, podemos obter a expressão do comprimento, da barra devido à variação de temperatura Δt. Sendo ΔL = L - Lo, obtemos:
𝑳 = 𝑳𝒐 + 𝜟𝑳
Exemplo 1: Um trilho de aço tem 100 m de comprimento a 10 °C. Qual o acréscimo de comprimento desse trilho quando a sua temperatura chega a 30 °C? (Dado: coeficiente de dilatação linear do aço: αaço = 1,1.10-5 °C-1).
Resolução do exemplo 1:
Sendo Lo = 100 m, Δt = 30 °C - 10 °C = 20 °C, αaço = 1,1.10-5 °C-1,
basta aplicarmos os valores nas expressão 𝛥𝐿 = 𝐿𝑜. 𝛼. 𝛥𝑡.
Assim, teremos que:
𝛥𝐿 = 100 . 1,1.10 − 5 . 20 ⟹ 𝜟𝑳 = 𝟎, 𝟎𝟐𝟐 𝒎
O coeficiente de dilatação linear de um sólido, embora varie pouco, só é constante dentro de
determinado intervalo de temperaturas. Por isso os dados da tabela a seguir se referem à
temperatura de 20 °C em torno da qual foram determinados.

Dilatação Superficial
A dilatação superficial leva em consideração a dilatação sofrida por uma determinada superfície. É
o que acontece, por exemplo, com uma chapa de metal delgada.
Para calcular a dilatação superficial utilizamos a seguinte fórmula:
𝜟𝑨 = 𝑨𝒐. 𝜷. 𝜟𝒕
Onde,
ΔA: Variação da área (m2 ou cm2);
A0: Área inicial (m2 ou cm2);
β: Coeficiente de dilatação superficial (ºC-1);
Δt: Variação de temperatura (ºC).
Importa destacar que o coeficiente de dilatação superficial (β) é igual a duas vezes o valor do
coeficiente de dilatação linear (α), ou seja:
𝜷 = 𝟐 . 𝜶
Exemplo 2: Um quadrado de lado 2 m é feito de um material cujo coeficiente de dilatação superficial
é igual a 1,6.10-4. Determine a variação de área deste quadrado quando aquecido em 80°C.
Resolução do exemplo 2: Sabendo que a área do quadrado é:
𝐴 = 𝑙𝑎𝑑𝑜. 𝑙𝑎𝑑𝑜 = 2 . 2 = 4 𝑚
Teremos que a área inicial do material será Ao = 4 m. Através da leitura do enunciado, temos que:
β = 1,6.10-4 e Δt = 80°C.
Substituindo na equação:
ΔA = 4 . 1,6 .10-4 . 80 ⟹ ΔA = 0,0512 m²
Dilatação Volumétrica
A dilatação volumétrica resulta do aumento no volume de um corpo, o que acontece, por exemplo,
com uma barra de ouro.
Para calcular a dilatação volumétrica utilizamos a seguinte fórmula:
𝜟𝑽 = 𝑽𝒐. 𝜸. 𝜟𝒕
Onde,
ΔV: Variação do volume (m3 ou cm3);
V0: Volume inicial (m3 ou cm3);
γ: Coeficiente de dilatação volumétrica (ºC-1);
Δt: Variação de temperatura (ºC).
Repare que o coeficiente de dilatação volumétrico (γ) é três vezes maior que coeficiente de
dilatação linear (α), ou seja:
𝜸 = 𝟑 . 𝜶
Exemplo 3: Uma substância, ao ser submetida a uma variação de temperatura de 80ºC, sofreu
dilatação, aumentado seu volume em 10L. Calcule o coeficiente de dilatação volumétrica dessa
substância. Considere o volume inicial Vi = 500L.
Resolução do exemplo 3: Por meio da leitura do enunciado da questão, podemos retirar as
seguintes informações: ΔV = 10L; Δt = 80°C e Vo = 500 L. Como discutido acima, podemos
encontrar o coeficiente de dilatação volumétrica, através da equação:
Substituindo os valores, teremos que:
Os olhos de emocionam de encanto
Ante as pinceladas do artistas Criador
Que se exibem em arranjos fascinantes
A beleza de vida em pétalas de flor.
MSc. Maria Nazaré Ribon Silva





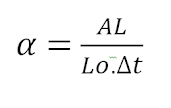




Nenhum comentário:
Postar um comentário